We capture the geometries of sand grains via Micro-CT scanning images. Instead of using conformal meshes, we discretize the grains using cubic elements that compose surrogate domains. We concern two main problems, i.e. imposing boundary conditions and frictional contacts. The shift domain method is implemented to apply Dirichlet boundary conditions under the framework of an updated Lagrangian algorithm to simulate the damage of the grain. We also develop an unbiased Nitsche’s algorithm for frictional contacts using an implicit material point method enhanced by level sets. With these techniques, we can:
1. generate databases (constitutive laws considering real shapes) for machine learning;
2. introduce realistic mechanical behaviors of assemblies of grains to the multi-scale modeling.
Some applications are as follows.
(1) Soil fabric (clay structures in microscopic scales)

Flocculated structure Dispersed structure
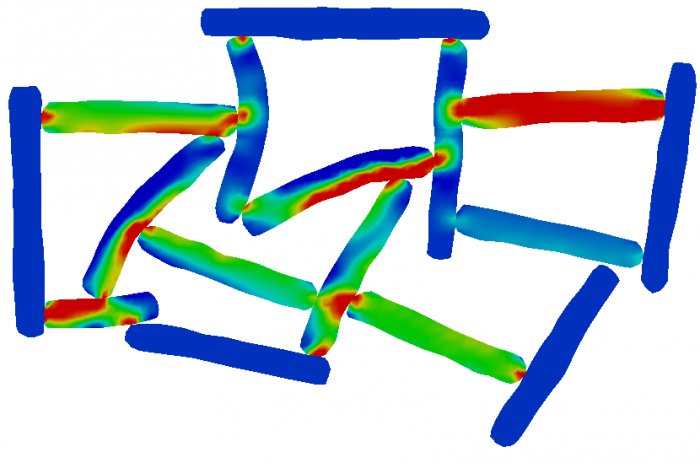
(2) Isotropic compression of an assembly of four grains reconstructed from scanning images
(3) Macroscopic behaviors of granular assemblies considering stress-fields of individual grains (please click the figure, it is an animation)


The framework of force chains Macroscopic constitutive laws
(4) Brazilian test for an elastic disc (also click the figure)

(5) Shift domain method to apply boundary conditions

Scanning image Level set Surrogate domain Damage field
创建: Jun 23, 2020 | 21:31
Faults are geological entities of rock where relative displacement can occur in the plane of the fault. During industrial activities such as disposal of waste water or CO2, fault slip may reactivate due to the changes in hydraulic pressures and deformations of the rock matrix. The motion of faults may threaten the stability of wells, even induce seismicity. Therefore, accurate and efficient simulation techniques are required to assess the potential for fault reactivation.
We employ the extended finite element method (X-FEM) to approximate different types of discontinuous physical fields, such as strong discontinuities for displacement and strong/weak discontinuities for pressure, and the interaction between fault surfaces is modeled using the
Mohr-Coulomb criterion. We assess the reactivation of various faults triggered by a change of pressure. We also implement a new integration scheme to eliminate the need for element partitioning to integrate discontinuous functions over elements.
Some results are as follows.
(1) Fluid flow within a domain containing jagged faults (integration without element-partitioning)
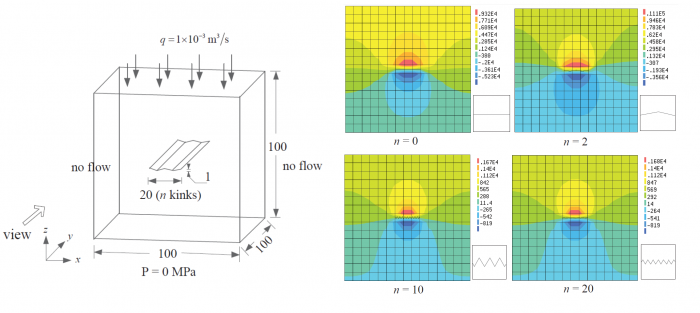
Numerical model Pressure distributions for various cases
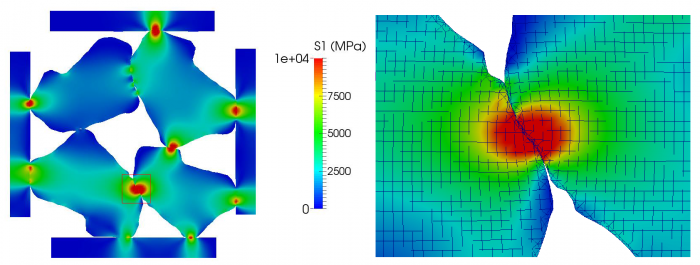
(2) Branched and intersecting faults

Comparison of meshes used in FEM and X-FEM
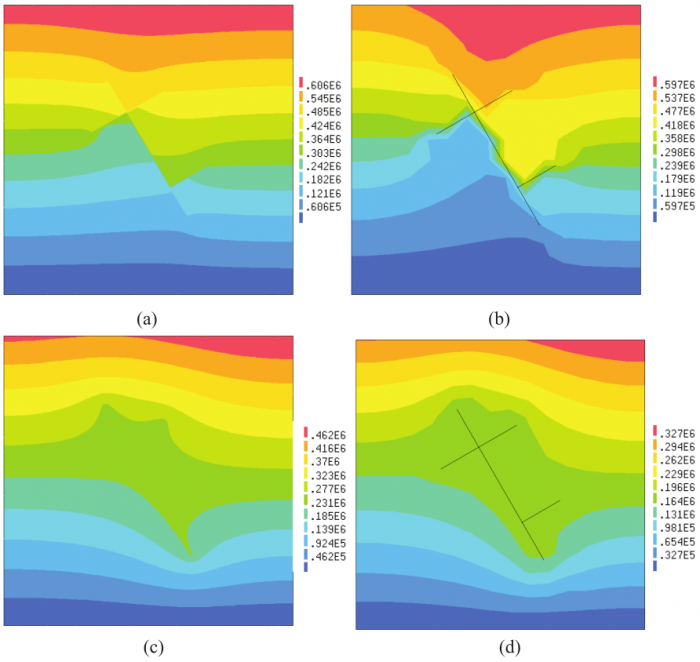
Comparisons of distributions of pressures using different methods
(3) Assessment of the reactivation of a typical fault

Numerical model


Distribution of pressure after 8 hours of the injection Displacement field
创建: Jun 24, 2020 | 15:15
The material point method (MPM) is a meshfree method that can alleviate the issue of mesh-distortion confronted in the FEM for large deformation problems. We develop a serious of models based on the MPM to simulate granular flows.
(1) Coupling of the MPM and the DEM for granular flows impacting simulations
We adopt the MPM to model granular flows and the deformable DEM to model blocks. Each block is treated as comprising nine material points to couple the MPM and DEM, and the acceleration of grid nodes arising from the contacts between granular material and blocks is projected to the discrete element nodes working as body forces. Some results are shown below (click the figure to see the animation).

(2) Two-phases MPM
We use two set material points representing solid and fluid, respectively to consider the hydro-mechanical coupling problems. An experiment is conducted as a reference for validation. The results are shown below.
Sliding surface in the experiment Plastic strain distributions in simulations
(3) Hierarchy multi-scale modelling framework for granular materials using the MPM and DEM
Under this multi-scale framework, each material point is connected with a representative volume element consisting of an assembly of spheres. We abandon the phenomenological constitutive laws of granular materials and directly extract the constitutive relationships for each RVE using the DEM. Thus, we can link the macroscopic behaviors (such as plastic strain) and the microscopic mechanisms (such as force chains).


Schematic of the modelling scheme Connections of the macroscopic plastic strain and local packings

Displacements of the collapse of the granular pile simulated using the multiscale modelling scheme.
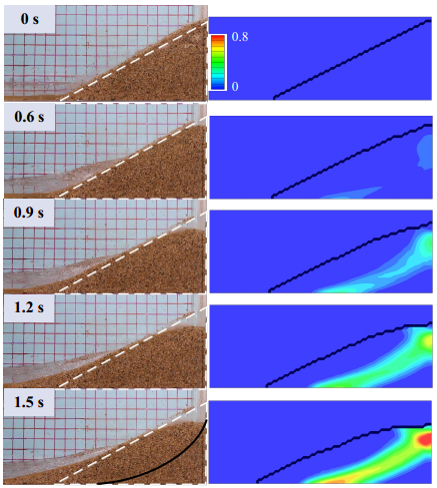
(4) Simulations of debris flows
We incorporate the domain terrain to simulate the process of a debris flow. The process is shown as flows (click the figure to see the animation)
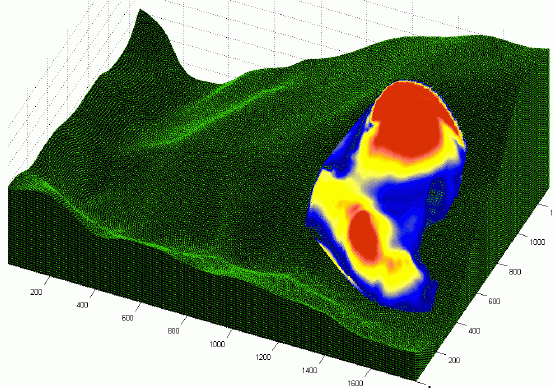
The process of debris flow (simulated by others using our code)
创建: Jun 26, 2020 | 09:12
Granular materials can behave like solids and fluids exhibiting complex mechanical behavirors. We conduct studies on the granular materials in the physical perspective to discover the physical mechanisms of the mechanical behaviors of granular materials. Thus, we can deepen our understandings on the mysterious materials.
(1) Kinematic and energy characteristic of a granular flow
We develop a plate shear model to study the kinematic and energy characteristics of granular flows. The inertial number is used to distinguish different flow regimes. Linear/angular velocity profiles, force chains and other qualities are compared for different regions.

(2) Structural signature for the solid-fluid transition
We summarize the popular structural analysis tools and classified them into different strategies. We adopt the radial tessellation to analyze the topological states and find that the fivefold symmetry is a critical structural signature. The region holding high fivefold symmetry is linked with the shear bands. Based on our understanding of mesoscopic structures, we define a structure unit to explain the transition between solid-like and fluid-like behaviors.

Summary of structural analysis tools

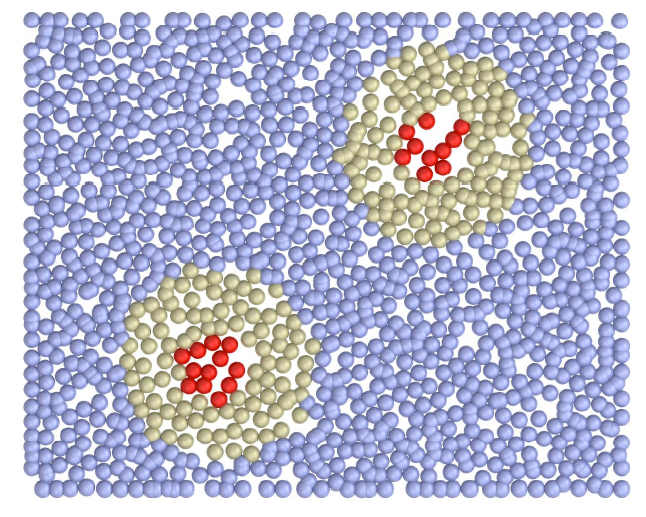
A structural granular assembly unit.
创建: Jun 27, 2020 | 16:37
In this project, we couple the FEM and DFM to develop a numerical model for crack propagation. The crack model is then combined with a fluid flow model to simulate the process of hydraulic fracturing.
(1) Crack propagation (click to see the animation)


Comparisons of simulations and experimental results (click to see the animation)
(2) Model of hydraulic fracturing and its application

Temporal evolution of hydraulic pressure during the fracturing process

An application: exploring of the effect of inhomogeneous sediment (click to see the results)
创建: Jun 27, 2020 | 20:49



























